Polynomial Class Reference

A one dimensional real polynomial. More...

#include <Polynomial.h>

Inheritance diagram for Polynomial:

List of all members.

Public Member Functions

Polynomial ()

Constructs an uninitialized instance of this class.

Polynomial (Array1D< double > &coeffs)

Constructs and initializes an intance of this class.

void initialize (Array1D< double > &coeffs)

Initializes this object.

void evaluate (double x)

Evaluates the function at $x$ .

double getFunctionValue ()

Gets the function value at the last evaluated point.

double getFunctionValue (double x)

This call doesn't calculate derivatives, only the function.

double getFirstDerivativeValue ()

Gets the function's first deriviate at the last evaluated point.

double getSecondDerivativeValue ()

Gets the function's second deriviative at the last evaluated point.

double getThirdDerivativeValue ()

double get_p_a (int ai)

double get_p2_xa (int ai)

double get_p3_xxa (int ai)

Array1D< double > getCoefficients ()

This gives us access to the coefficients that this polynomial uses.

Array1D< Complex > getRoots ()

Gets the roots of the polynomial.

void operator= (Polynomial rhs)

Sets this polynomial equal to another one.

int getNumberCoefficients ()

Gets the number of coefficients in the polynomial.

double getCoefficient (int i)

Gets the ith coefficient of the polynomial.

void print (ostream &strm)

Write out a string that represents the polynomial.

double Brent_fmin (double ax, double bx, double tol)

double function (double x)

double minimum (double left, double right)

Private Member Functions

void initialize ()

Initialize all of the member variables of this object.

double evaluate (double x, Array1D< double > &coeffs)

Evaluates a polynomial at $x$ defined by the entered coefficients.

void evaluateAll (double x, Array1D< double > &coeffs)

Evaluates a polynomial at $x$ defined by the entered coefficients.

void laguer (Array1D< Complex > &a, int m, Complex &x, int *its, bool *calcOK)

Given a complex point $x$ and a polynomial with complex coefficients, converges $x$ to the root of the polynomial, within achievable roundoff limits, using Laguerre's method.

Array1D< Complex > zroots (Array1D< Complex > &a, bool polish, bool *calcOK)

Finds the roots of a polynomial with complex coefficients using Laguerre's method.

Private Attributes

Array1D< double > coefficients

Coefficients of the polynomial.

Array1D< double > firstDerivativeCoefficients

Coefficients of the polynomial's first derivative.

Array1D< double > secondDerivativeCoefficients

Coefficients of the polynomial's second derivative.

Array1D< double > thirdDerivativeCoefficients

Coefficients of the polynomial's third derivative.

double f

Last calculated function value.

double df

Last calculated function first derivative value.

double d2f

Last calculated function second derivative value.

double d3f

Last calculated function third derivative value.

double x

Last evaluated x value.

bool evaluatedF

Has the function value been calculated for the last evaluated x value.

bool evaluatedDF

Has the function first derivative value been calculated for the last evaluated x value.

bool evaluatedD2F

Has the function second derivative value been calculated for the last evaluated x value.

Detailed Description

A one dimensional real polynomial.

$P(x) = \sum^{n}_{i=0}c_{i}x^{i}$

Definition at line 28 of file Polynomial.h.

Constructor & Destructor Documentation

Polynomial::Polynomial ( )

Constructs an uninitialized instance of this class.

Definition at line 35 of file Polynomial.cpp.

References initialize().

Polynomial::Polynomial ( Array1D< double > & coeffs )

Constructs and initializes an intance of this class.

Parameters:

coeffs

set of polynomial coefficients to use for the polynomial.

Definition at line 40 of file Polynomial.cpp.

References initialize().

Member Function Documentation

void Polynomial::initialize ( Array1D< double > & coeffs )

Initializes this object.

Parameters:

coeffs

set of polynomial coefficients to use for the polynomial.

Definition at line 65 of file Polynomial.cpp.

References Array1D< T >::allocate(), coefficients, Array1D< T >::dim1(), firstDerivativeCoefficients, secondDerivativeCoefficients, and thirdDerivativeCoefficients.

Referenced by QMCElectronNucleusCuspParameters::calculateSigmaSq(), QMCElectronNucleusCusp::determineRc(), QMCElectronNucleusCuspParameters::fitReplacementOrbital(), PadeCorrelationFunction::initializeParameters(), JuliusCorrelationFunction::initializeParameters(), FixedCuspPadeCorrelationFunction::initializeParameters(), and Cambridge2CorrelationFunction::initializeParameters().

void Polynomial::evaluate ( double x ) [virtual]

Evaluates the function at $x$ .

Parameters:

x

point to evaluate the function.

Implements FunctionR1toR1.

Definition at line 95 of file Polynomial.cpp.

References evaluatedD2F, evaluatedDF, and evaluatedF.

Referenced by QMCElectronNucleusCuspParameters::calculateLocalEnergy(), QMCElectronNucleusCusp::determineRc(), PadeCorrelationFunction::evaluate(), JuliusCorrelationFunction::evaluate(), FixedCuspPadeCorrelationFunction::evaluate(), Cambridge2CorrelationFunction::evaluate(), QMCElectronNucleusCuspParameters::evaluateReplacementOrbital(), QMCElectronNucleusCuspParameters::findMaxDeviation(), getFunctionValue(), Cambridge2CorrelationFunction::getFunctionValue(), getThirdDerivativeValue(), and QMCElectronNucleusCuspParameters::printParameters().

double Polynomial::getFunctionValue ( ) [virtual]

Gets the function value at the last evaluated point.

Returns:: function value.

Implements FunctionR1toR1.

Definition at line 146 of file Polynomial.cpp.

References coefficients, evaluateAll(), evaluatedF, f, and x.

double Polynomial::getFunctionValue ( double x )

This call doesn't calculate derivatives, only the function.

It's supposed to be faster than calling evaluate, which does calculate the first 2 derivatives.

Definition at line 157 of file Polynomial.cpp.

References coefficients, and evaluate().

double Polynomial::getFirstDerivativeValue ( ) [virtual]

Gets the function's first deriviate at the last evaluated point.

Returns:: function's deriviative value.

Implements FunctionR1toR1.

Definition at line 167 of file Polynomial.cpp.

References coefficients, df, evaluateAll(), evaluatedDF, and x.

Referenced by QMCElectronNucleusCuspParameters::calculateLocalEnergy(), PadeCorrelationFunction::evaluate(), JuliusCorrelationFunction::evaluate(), FixedCuspPadeCorrelationFunction::evaluate(), Cambridge2CorrelationFunction::evaluate(), QMCElectronNucleusCuspParameters::evaluateReplacementOrbital(), FixedCuspPadeCorrelationFunction::get_p2_xa(), and FixedCuspPadeCorrelationFunction::get_p3_xxa().

double Polynomial::getSecondDerivativeValue ( ) [virtual]

Gets the function's second deriviative at the last evaluated point.

Returns:: function's second derivative value.

Implements FunctionR1toR1.

Definition at line 184 of file Polynomial.cpp.

References coefficients, d2f, evaluateAll(), evaluatedD2F, and x.

Referenced by QMCElectronNucleusCuspParameters::calculateLocalEnergy(), PadeCorrelationFunction::evaluate(), JuliusCorrelationFunction::evaluate(), FixedCuspPadeCorrelationFunction::evaluate(), Cambridge2CorrelationFunction::evaluate(), QMCElectronNucleusCuspParameters::evaluateReplacementOrbital(), and FixedCuspPadeCorrelationFunction::get_p3_xxa().

double Polynomial::getThirdDerivativeValue ( )

Definition at line 195 of file Polynomial.cpp.

References d3f, evaluate(), thirdDerivativeCoefficients, and x.

Referenced by Cambridge2CorrelationFunction::evaluate().

double Polynomial::get_p_a ( int ai )

Definition at line 162 of file Polynomial.cpp.

References x.

Referenced by FixedCuspPadeCorrelationFunction::get_p2_xa(), Cambridge2CorrelationFunction::get_p2_xa(), FixedCuspPadeCorrelationFunction::get_p3_xxa(), Cambridge2CorrelationFunction::get_p3_xxa(), FixedCuspPadeCorrelationFunction::get_p_a(), and Cambridge2CorrelationFunction::get_p_a().

double Polynomial::get_p2_xa ( int ai )

Definition at line 178 of file Polynomial.cpp.

References x.

Referenced by FixedCuspPadeCorrelationFunction::get_p2_xa(), Cambridge2CorrelationFunction::get_p2_xa(), FixedCuspPadeCorrelationFunction::get_p3_xxa(), and Cambridge2CorrelationFunction::get_p3_xxa().

double Polynomial::get_p3_xxa ( int ai )

Definition at line 202 of file Polynomial.cpp.

References x.

Referenced by FixedCuspPadeCorrelationFunction::get_p3_xxa(), and Cambridge2CorrelationFunction::get_p3_xxa().

Array1D< double > Polynomial::getCoefficients ( )

This gives us access to the coefficients that this polynomial uses.

Reimplemented in PowerSeries.

Definition at line 217 of file Polynomial.cpp.

References coefficients.

Referenced by QMCElectronNucleusCuspParameters::calculateSigmaSq(), PadeCorrelationFunction::getDenominatorCoeffs(), FixedCuspPadeCorrelationFunction::getDenominatorCoeffs(), Cambridge2CorrelationFunction::getDenominatorCoeffs(), PadeCorrelationFunction::getNumeratorCoeffs(), JuliusCorrelationFunction::getNumeratorCoeffs(), FixedCuspPadeCorrelationFunction::getNumeratorCoeffs(), Cambridge2CorrelationFunction::getNumeratorCoeffs(), and QMCElectronNucleusCuspParameters::printParameters().

Array1D< Complex > Polynomial::getRoots ( )

Gets the roots of the polynomial.

Returns:: roots of the polynomial.

Exceptions:

Exception

if problems were encounted during the root calculation.

If the highest order terms have 0 for a coefficient, then we have fewer roots.

Definition at line 243 of file Polynomial.cpp.

References coefficients, Array1D< T >::dim1(), and zroots().

Referenced by QMCElectronNucleusCuspParameters::calculateSigmaSq(), PadeCorrelationFunction::getPoles(), FixedCuspPadeCorrelationFunction::getPoles(), and QMCPolynomial::hasNonNegativeZeroes().

void Polynomial::operator= ( Polynomial rhs )

Sets this polynomial equal to another one.

Parameters:

rhs

polynomial to set this one equal to

Definition at line 46 of file Polynomial.cpp.

References coefficients, and initialize().

int Polynomial::getNumberCoefficients ( )

Gets the number of coefficients in the polynomial.

This is one larger than the order of the polynomial.

Returns:: number of coefficients in the polynomial.

Reimplemented in PowerSeries.

Definition at line 207 of file Polynomial.cpp.

References coefficients, and Array1D< T >::dim1().

Referenced by FixedCuspPadeCorrelationFunction::get_p2_xa(), FixedCuspPadeCorrelationFunction::get_p3_xxa(), and FixedCuspPadeCorrelationFunction::get_p_a().

double Polynomial::getCoefficient ( int i )

Gets the ith coefficient of the polynomial.

Where the polynomial is defined such that

$P(x) = \sum^{n}_{i=0}c_{i}x^{i}$

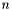where $n$ is the order of the polynomial and $c_{i}$ is the ith coefficient.

Parameters:

i

index of the coefficient to return.

Returns:: ith coefficient of the polynomial.

Reimplemented in PowerSeries.

Definition at line 212 of file Polynomial.cpp.

References coefficients.

void Polynomial::print ( ostream & strm )

Write out a string that represents the polynomial.

Reimplemented in PowerSeries.

Definition at line 222 of file Polynomial.cpp.

References coefficients, and Array1D< T >::dim1().

Referenced by operator<<(), and FixedCuspPadeCorrelationFunction::print().

void Polynomial::initialize ( ) [private]

Initialize all of the member variables of this object.

Reimplemented in PowerSeries.

Definition at line 52 of file Polynomial.cpp.

References d2f, df, evaluatedD2F, evaluatedDF, evaluatedF, f, and x.

Referenced by operator=(), and Polynomial().

double Polynomial::evaluate	(	double	x,
		Array1D< double > &	coeffs
	)			`[private]`

Evaluates a polynomial at $x$ defined by the entered coefficients.

Parameters:

	x	point to evaluate the polynomial at.
	coeffs	coefficients describing the polynomial being evaluated. These are ordered from smallest to largest powers of .

Returns:: value of the polynomial defined by coeffs at x.

Definition at line 103 of file Polynomial.cpp.

References Array1D< T >::dim1().

void Polynomial::evaluateAll	(	double	x,
		Array1D< double > &	coeffs
	)			`[private]`

Evaluates a polynomial at $x$ defined by the entered coefficients.

In addition, it evaluates the 1st two derivatives of that polynomial. It stores the results in f, df, and d2f from this class.

Parameters:

	x	point to evaluate the polynomial at.
	coeffs	coefficients describing the polynomial being evaluated. These are ordered from smallest to largest powers of .

Reimplemented in PowerSeries.

Definition at line 122 of file Polynomial.cpp.

References d2f, df, Array1D< T >::dim1(), evaluatedD2F, evaluatedDF, evaluatedF, and f.

Referenced by getFirstDerivativeValue(), getFunctionValue(), and getSecondDerivativeValue().

void Polynomial::laguer	(	Array1D< Complex > &	a,
		int	m,
		Complex &	x,
		int *	its,
		bool *	calcOK
	)			`[private]`

Given a complex point $x$ and a polynomial with complex coefficients, converges $x$ to the root of the polynomial, within achievable roundoff limits, using Laguerre's method.

This method can be used to refine the roots of a polynomial with either real or complex coefficients. This was adapted from "Numerical Recipes in C".

Parameters:

	a	complex coefficients of the polynomial ordered from lowest to highest powers of x.
	m	degree of the polynomial. This is one less than the number of coefficients.
	x	complex point to refine to the polynomial's root.
	its	number of iterations taken to refine the root.
	calcOK	`true` if there were no problems during the calculation and `false` if too many iterations were performed. When this happens try a different starting guess for the root.

Definition at line 291 of file Polynomial.cpp.

References Complex::abs(), EPSS, f, Complex::imaginary(), MAXIT, MR, MT, Complex::real(), and Complex::squareroot().

Referenced by zroots().

Array1D< Complex > Polynomial::zroots	(	Array1D< Complex > &	a,
		bool	polish,
		bool *	calcOK
	)			`[private]`

Finds the roots of a polynomial with complex coefficients using Laguerre's method.

This was adapted from "Numerical Recipes in C".

Parameters:

	a	complex coefficients of the polynomial ordered from lowest to highest powers of x.
	polish	`true` if the roots are going to be polished using Laguerre's method and `false` if these roots will be given to another routine to polish.
	calcOK	`true` if there were no problems during the calculation and `false` if too many iterations were performed while calculating one of the roots.

Returns:: roots of the polynomial described by a.

Definition at line 358 of file Polynomial.cpp.

References Array1D< T >::dim1(), EPS, Complex::imaginary(), laguer(), Complex::real(), and x.

Referenced by getRoots().

double FunctionR1toR1::Brent_fmin	(	double	ax,
		double	bx,
		double	tol
	)			`[inherited]`

Definition at line 81 of file FunctionR1toR1.cpp.

References FunctionR1toR1::function().

Referenced by FunctionR1toR1::minimum().

double FunctionR1toR1::function ( double x ) [inherited]

Definition at line 209 of file FunctionR1toR1.cpp.

References FunctionR1toR1::evaluate(), and FunctionR1toR1::getFunctionValue().

Referenced by FunctionR1toR1::Brent_fmin(), and QMCEigenSearch::get_a_diag().

double FunctionR1toR1::minimum	(	double	left,
		double	right
	)			`[inherited]`

Definition at line 215 of file FunctionR1toR1.cpp.

References FunctionR1toR1::Brent_fmin().

Referenced by QMCEigenSearch::get_a_diag().

Member Data Documentation

Array1D<double> Polynomial::coefficients [private]

Coefficients of the polynomial.

They are arranged from smallest to largest powers of x.

Definition at line 35 of file Polynomial.h.

Referenced by getCoefficient(), getCoefficients(), getFirstDerivativeValue(), getFunctionValue(), getNumberCoefficients(), getRoots(), getSecondDerivativeValue(), initialize(), operator=(), and print().

Array1D<double> Polynomial::firstDerivativeCoefficients [private]

Coefficients of the polynomial's first derivative.

They are arranged from smallest to largest powers of x.

Definition at line 41 of file Polynomial.h.

Referenced by initialize().

Array1D<double> Polynomial::secondDerivativeCoefficients [private]

Coefficients of the polynomial's second derivative.

They are arranged from smallest to largest powers of x.

Definition at line 47 of file Polynomial.h.

Referenced by initialize().

Array1D<double> Polynomial::thirdDerivativeCoefficients [private]

Coefficients of the polynomial's third derivative.

They are arranged from smallest to largest powers of x.

Definition at line 53 of file Polynomial.h.

Referenced by getThirdDerivativeValue(), and initialize().

double Polynomial::f [private]

Last calculated function value.

Definition at line 58 of file Polynomial.h.

Referenced by evaluateAll(), getFunctionValue(), initialize(), and laguer().

double Polynomial::df [private]

Last calculated function first derivative value.

Definition at line 63 of file Polynomial.h.

Referenced by evaluateAll(), getFirstDerivativeValue(), and initialize().

double Polynomial::d2f [private]

Last calculated function second derivative value.

Definition at line 68 of file Polynomial.h.

Referenced by evaluateAll(), getSecondDerivativeValue(), and initialize().

double Polynomial::d3f [private]

Last calculated function third derivative value.

Definition at line 73 of file Polynomial.h.

Referenced by getThirdDerivativeValue().

double Polynomial::x [private]

Last evaluated x value.

Definition at line 78 of file Polynomial.h.

Referenced by get_p2_xa(), get_p3_xxa(), get_p_a(), getFirstDerivativeValue(), getFunctionValue(), getSecondDerivativeValue(), getThirdDerivativeValue(), initialize(), and zroots().

bool Polynomial::evaluatedF [private]

Has the function value been calculated for the last evaluated x value.

Definition at line 84 of file Polynomial.h.

Referenced by evaluate(), evaluateAll(), getFunctionValue(), and initialize().

bool Polynomial::evaluatedDF [private]

Has the function first derivative value been calculated for the last evaluated x value.

Definition at line 90 of file Polynomial.h.

Referenced by evaluate(), evaluateAll(), getFirstDerivativeValue(), and initialize().

bool Polynomial::evaluatedD2F [private]

Has the function second derivative value been calculated for the last evaluated x value.

Definition at line 96 of file Polynomial.h.

Referenced by evaluate(), evaluateAll(), getSecondDerivativeValue(), and initialize().

The documentation for this class was generated from the following files:


Public Member Functions
	Polynomial ()
	Constructs an uninitialized instance of this class.
	Polynomial (Array1D< double > &coeffs)
	Constructs and initializes an intance of this class.
void	initialize (Array1D< double > &coeffs)
	Initializes this object.
void	evaluate (double x)
	Evaluates the function at .
double	getFunctionValue ()
	Gets the function value at the last evaluated point.
double	getFunctionValue (double x)
	This call doesn't calculate derivatives, only the function.
double	getFirstDerivativeValue ()
	Gets the function's first deriviate at the last evaluated point.
double	getSecondDerivativeValue ()
	Gets the function's second deriviative at the last evaluated point.
double	getThirdDerivativeValue ()
double	get_p_a (int ai)
double	get_p2_xa (int ai)
double	get_p3_xxa (int ai)
Array1D< double >	getCoefficients ()
	This gives us access to the coefficients that this polynomial uses.
Array1D< Complex >	getRoots ()
	Gets the roots of the polynomial.
void	operator= (Polynomial rhs)
	Sets this polynomial equal to another one.
int	getNumberCoefficients ()
	Gets the number of coefficients in the polynomial.
double	getCoefficient (int i)
	Gets the ith coefficient of the polynomial.
void	print (ostream &strm)
	Write out a string that represents the polynomial.
double	Brent_fmin (double ax, double bx, double tol)
double	function (double x)
double	minimum (double left, double right)
Private Member Functions
void	initialize ()
	Initialize all of the member variables of this object.
double	evaluate (double x, Array1D< double > &coeffs)
	Evaluates a polynomial at defined by the entered coefficients.
void	evaluateAll (double x, Array1D< double > &coeffs)
	Evaluates a polynomial at defined by the entered coefficients.
void	laguer (Array1D< Complex > &a, int m, Complex &x, int its, bool calcOK)
	Given a complex point and a polynomial with complex coefficients, converges to the root of the polynomial, within achievable roundoff limits, using Laguerre's method.
Array1D< Complex >	zroots (Array1D< Complex > &a, bool polish, bool *calcOK)
	Finds the roots of a polynomial with complex coefficients using Laguerre's method.
Private Attributes
Array1D< double >	coefficients
	Coefficients of the polynomial.
Array1D< double >	firstDerivativeCoefficients
	Coefficients of the polynomial's first derivative.
Array1D< double >	secondDerivativeCoefficients
	Coefficients of the polynomial's second derivative.
Array1D< double >	thirdDerivativeCoefficients
	Coefficients of the polynomial's third derivative.
double	f
	Last calculated function value.
double	df
	Last calculated function first derivative value.
double	d2f
	Last calculated function second derivative value.
double	d3f
	Last calculated function third derivative value.
double	x
	Last evaluated x value.
bool	evaluatedF
	Has the function value been calculated for the last evaluated x value.
bool	evaluatedDF
	Has the function first derivative value been calculated for the last evaluated x value.
bool	evaluatedD2F
	Has the function second derivative value been calculated for the last evaluated x value.